Una manera simple de expresar el ordenamiento de burbuja en pseudocódigo es la siguiente:
La burbuja son dos términos de la lista seguidos, j y j+1, que se comparan, si el primero es menor que el segundo sus valores se intercambian.
Esta comparación se repite en el centro de los dos bucles, dando lugar a la postre a una lista ordenada, puede verse que el número de repeticiones sola depende de n, y no del orden de los términos, esto es si pasamos al algoritmo una lista ya ordenada, realizara todas las comparaciones exactamente igual que para una lista no ordenada, esta es una característica de este algoritmo, luego veremos una variante que evita este problema.
Ordenamiento Shell
De Wikipedia, la enciclopedia libre
El ordenamiento Shell (Shell sort en inglés) es un algoritmo de ordenamiento. El método se denomina Shell en honor de su inventor Donald Shell. Su implementación original, requiere O(n2) comparaciones e intercambios en el peor caso. Un cambio menor presentado en el libro de V. Pratt produce una implementación con un rendimiento de O(nlog2 n) en el peor caso. Esto es mejor que las O(n2) comparaciones requeridas por algoritmos simples pero peor que el óptimo O(n log n). Aunque es fácil desarrollar un sentido intuitivo de cómo funciona este algoritmo, es muy difícil analizar su tiempo de ejecución.El Shell sort es una generalización del ordenamiento por inserción, teniendo en cuenta dos observaciones:
- El ordenamiento por inserción es eficiente si la entrada está "casi ordenada".
- El ordenamiento por inserción es ineficiente, en general, porque mueve los valores sólo una posición cada vez.
Ejemplo
Considere un pequeño valor que está inicialmente almacenado en el final del vector. Usando un ordenamiento O(n2) como el ordenamiento de burbuja o el ordenamiento por inserción, tomará aproximadamente n comparaciones e intercambios para mover este valor hacia el otro extremo del vector. El Shell sort primero mueve los valores usando tamaños de espacio gigantes, de manera que un valor pequeño se moverá bastantes posiciones hacia su posición final, con sólo unas pocas comparaciones e intercambios.Uno puede visualizar el algoritmo Shell sort de la siguiente manera: coloque la lista en una tabla y ordene las columnas (usando un ordenamiento por inserción). Repita este proceso, cada vez con un número menor de columnas más largas. Al final, la tabla tiene sólo una columna. Mientras que transformar la lista en una tabla hace más fácil visualizarlo, el algoritmo propiamente hace su ordenamiento en contexto (incrementando el índice por el tamaño de paso, esto es usando
i += tamaño_de_paso en vez de i++).Por ejemplo, considere una lista de números como
[ 13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10 ]. Si comenzamos con un tamaño de paso de 5, podríamos visualizar esto dividiendo la lista de números en una tabla con 5 columnas. Esto quedaría así:13 14 94 33 82 25 59 94 65 23 45 27 73 25 39 10Entonces ordenamos cada columna, lo que nos da
10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45Cuando lo leemos de nuevo como una única lista de números, obtenemos
[ 10 14 73 25 23 13 27 94 33 39 25 59 94 65 82 45 ]. Aquí, el 10 que estaba en el extremo final, se ha movido hasta el extremo inicial. Esta lista es entonces de nuevo ordenada usando un ordenamiento con un espacio de 3 posiciones, y después un ordenamiento con un espacio de 1 posición (ordenamiento por inserción simple).El Shell sort lleva este nombre en honor a su inventor, Donald Shell, que lo publicó en 1959. Algunos libros de texto y referencias antiguas le llaman ordenación "Shell-Metzner" por Marlene Metzner Norton, pero según Metzner, "No tengo nada que ver con el algoritmo de ordenamiento, y mi nombre nunca debe adjuntarse a éste."
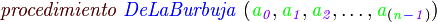
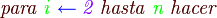
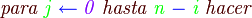


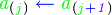

No hay comentarios:
Publicar un comentario